اشتہارات
بھاسکر، بھاسکر فارمولا
بھاسکرا کو ہم سب ریاضی کے فارمولے کے طور پر جانتے ہیں، لیکن کیا آپ جانتے ہیں کہ اس عظیم ریاضی دان کے نام کے حامل اس فارمولے کا خالق کون تھا؟ کیا آپ بھاسکر فارمولے کا حساب لگانا بھی جانتے ہیں؟
اگر آپ دونوں چیزوں میں سے کسی ایک کو بھی اچھی طرح سے نہیں جانتے ہیں اور یہ اور بھاسکرا کے بارے میں بہت کچھ جاننا چاہتے ہیں، تو آپ صحیح جگہ پر ہیں، اس مضمون میں ہمارے ساتھ رہیں اور ریاضی اور اس فارمولے کے ارد گرد کی تاریخ کے بارے میں اپنے علم میں اضافہ کریں۔ .
اشتہارات
بھاسکرا کون تھا؟
بھاسکر ایک ہندوستانی ریاضی دان، نجومی، ماہر فلکیات اور استاد تھے۔ وہ دوسری ڈگری کی مساوات میں لاگو ریاضیاتی فارمولہ بنانے کے لیے مشہور ہوا، حالانکہ اس حقیقت کے حوالے سے تنازعہ موجود ہے۔
بھاسکرا ہندوستان کے شہر وجے پورہ میں پیدا ہوا تھا، جہاں ریاضی دانوں کی ایک بہترین روایت ہے۔ ان کے والد ایک ماہر فلکیات تھے اور انہیں ریاضی اور فلکیات کے اصول سکھاتے تھے۔
وہ ریاضی کے ایک مشہور اسکول، اجین میں فلکیاتی رصد گاہ کے سربراہ تھے۔ بھاسکرا الجبرا کے مطالعہ کا ماہر تھا، جس کی وجہ سے وہ مساوات اور عددی نظام میں اپنی تحقیق کو مزید گہرا کرنے میں کامیاب ہوا۔
اشتہارات
بھاسکرا نے مساوات میں مربع جڑ کے سوال پر کام کیا، یہ جانتے ہوئے کہ چوکور مساوات کو حل کرنے میں دو جڑیں ہیں، لیکن کوئی ٹھوس ریکارڈ نہیں ہے کہ بھاسکر کا معروف فارمولا دراصل اس کا تھا۔ اس کی وجہ یہ ہے کہ 16ویں صدی تک مساوات میں حروف ہوتے تھے، جو اس صدی کے بعد فرانسیسی ریاضی دان François Viète نے استعمال کیا۔
بھاسکرا کا فارمولا اور اس کی تاریخ
بھاسکرا کا فارمولا نام ریاضی دان بھاسکارا اکاریا کو خراج عقیدت پیش کرنے کے لیے بنایا گیا تھا۔ وہ ایک ہندوستانی ریاضی دان، استاد، نجومی اور ماہر فلکیات تھے، جنہیں 12ویں صدی کا سب سے اہم ریاضی دان اور ہندوستان میں قرون وسطی کے آخری اہم ریاضی دان سمجھا جاتا تھا۔
بھاسکر کے فارمولے کو عام فارمولہ ax² + bx + c = 0 کے ساتھ چوکور مساوات کو حل کرنے کے لیے استعمال کیا جاتا ہے، حقیقی عدد کے ساتھ، ≠ 0 کے ساتھ۔ یہ اس فارمولے کے ذریعے ہے کہ ہم رقم (S) اور مصنوع کے لیے ایک اظہار نکال سکتے ہیں۔ P ) دوسری ڈگری مساوات کی جڑوں کا۔
بھاسکر فارمولا کیا ہے؟
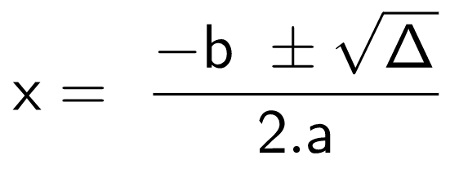
یہ بھاسکر فارمولہ دوسری ڈگری مساوات کے عمومی فارمولے سے نکلا ہے۔
ax2 + bx + c = 0
غیر صفر کے ساتھ؛
سب سے پہلے، ہم حساب کے تمام اراکین کو 4a سے ضرب دیتے ہیں:
4a2x2 + 4abx + 4ac = 0;
پھر ہم دونوں میں b2 شامل کرتے ہیں، جیسا کہ ذیل کی مثال میں ہے۔
4a2x2 + 4abx + 4ac + b2 = b2;
اس کے بعد، ہم دوبارہ منظم کرتے ہیں:
4a2x2 + 4abx + b2 = b2 – 4ac
اگر آپ دیکھتے ہیں، پہلا رکن ایک مکمل مربع ترنومیئل ہے:
(2ax + b)² = b² – 4ac
ہم دونوں اطراف کا مربع جڑ لیتے ہیں اور منفی اور مثبت جڑ کے امکان کو متعارف کراتے ہیں۔ پھر ہم نامعلوم ایکس کو الگ کرتے ہیں اور بس۔
