HIRDETÉSEK
Bhaskara, Bhaskara formula
Mindannyian ismerjük Bhaskarát matematikai képletként, de tudod, hogy ki volt ennek a képletnek a megalkotója, amely ennek a nagyszerű matematikusnak a nevét viseli? Azt is tudod, hogyan kell kiszámítani a Bhaskara képletet?
Ha a két dolog egyikét sem ismeri nagyon jól, és szeretné megtudni ezt és még sok minden mást Bhaskaráról, akkor jó helyen jár, tartson velünk ebben a cikkben, és bővítse ismereteit a matematikáról és a képletet körülvevő történelemről .
HIRDETÉSEK
Ki volt Bhaskara?
Bhaskara indiai matematikus, asztrológus, csillagász és tanár volt. A 2. fokú egyenletben alkalmazott matematikai képlet megalkotásával vált ismertté, bár ezzel kapcsolatban viták vannak.
Bhaskara az indiai Vijayapura városában született, egy olyan helyen, ahol a matematikusok kiváló hagyományai vannak. Édesapja csillagász volt, és megtanította neki a matematika és a csillagászat alapelveit.
Az újjaini csillagászati obszervatórium vezetője volt, egy jól ismert matematikai iskola. Bhaskara az algebratanulmányok specialistája volt, ami arra késztette, hogy elmélyítse az egyenletek és numerikus rendszerek kutatását.
HIRDETÉSEK
Bhaskara az egyenletek négyzetgyökének kérdésén dolgozott, tudván, hogy a másodfokú egyenlet megoldásában két gyök létezik, de nincsenek szilárd feljegyzések arról, hogy Bhaskara jól ismert képlete valójában az övé volt. Ennek az az oka, hogy a 16. századig az egyenletekben betűk voltak, amelyet a század után François Viète francia matematikus használt.
Bhaskara képlete és története
A Bhaskara's Formula nevet Bhaskara Akaria matematikus tiszteletére hozták létre. Indiai matematikus, tanár, asztrológus és csillagász volt, a 12. század legjelentősebb matematikusának és India utolsó jelentős középkori matematikusának tartották.
Bhaskara képletét másodfokú egyenletek megoldására használják az ax² + bx + c = 0 általános képlettel, valós együtthatókkal, ahol a ≠ 0. Ezen a képleten keresztül következtethetünk egy kifejezést az összegre (S) és a szorzatra ( P ) a 2. fokú egyenlet gyökeinek.
Mi a Bhaskara formula?
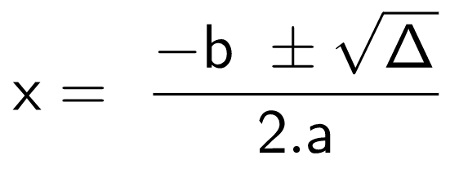
Ez a Bhaskara-képlet a 2. fokú egyenletek általános képletéből származik.
ax2 + bx + c = 0
nem nullával;
Először a számítás összes tagját megszorozzuk 4a-val:
4a2x2 + 4abx + 4ac = 0;
Ezután mindkettőhöz hozzáadjuk a b2-t, mint az alábbi példában.
4a2x2 + 4abx + 4ac + b2 = b2;
Ezt követően újra csoportosítunk:
4a2x2 + 4abx + b2 = b2 – 4ac
Ha észreveszi, az első tag egy tökéletes négyzetháromtag:
(2ax + b)² = b² – 4ac
Mindkét oldal négyzetgyökét vesszük, és bevezetjük egy negatív és egy pozitív gyök lehetőségét. Ezután elkülönítjük az ismeretlen x-et és ennyi.
