REKLAMLAR
Bhaskara, Bhaskara Formülü
Hepimiz Bhaskara'yı matematik formülü olarak biliyoruz ama bu büyük matematikçinin adını taşıyan bu formülün yaratıcısının kim olduğunu biliyor musunuz? Bhaskara formülünü nasıl hesaplayacağınızı da biliyor musunuz?
Her iki şeyi de çok iyi bilmiyorsanız ve Bhaskara hakkında bunu ve daha fazlasını öğrenmek istiyorsanız, doğru yerdesiniz, bu makalede bizimle kalın ve matematik ve bu formülü çevreleyen tarih hakkındaki bilginizi artırın. .
REKLAMLAR
Bhaskara kimdi?
Bhaskara Hintli bir matematikçi, astrolog, astronom ve öğretmendi. Bu konuda tartışmalar olmasına rağmen 2. derece denklemde uygulanan matematiksel formülü oluşturmasıyla tanındı.
Bhaskara, mükemmel bir matematikçi geleneğine sahip olan Hindistan'ın Vijayapura şehrinde doğdu. Babası bir astronomdu ve ona matematik ve astronominin ilkelerini öğretti.
Tanınmış bir matematik okulu olan Ujjain'deki astronomi gözlemevinin başkanıydı. Bhaskara cebir çalışmalarında uzmandı ve bu da onun araştırmalarını denklemler ve sayısal sistemler üzerinde derinleştirmesine yol açtı.
REKLAMLAR
Bhaskara, ikinci dereceden denklemin çözümünde iki kök olduğunu bilerek denklemlerdeki karekök sorusu üzerinde çalıştı, ancak Bhaskara'nın iyi bilinen formülünün aslında ona ait olduğuna dair sağlam kayıtlar yok. Çünkü 16. yüzyıla kadar denklemlerde harfler vardı ve bu yüzyıldan sonra Fransız matematikçi François Viète tarafından kullanılmaya başlandı.
Bhaskara'nın formülü ve tarihi
Bhaskara'nın Formülü adı matematikçi Bhaskara Akaria'ya saygı duruşunda bulunmak için yaratıldı. 12. yüzyılın en önemli matematikçisi ve Hindistan'daki son önemli ortaçağ matematikçisi olarak kabul edilen Hintli bir matematikçi, öğretmen, astrolog ve astronomdu.
Bhaskara formülü, ax² + bx + c = 0 genel formülüne sahip, gerçek katsayılı ve a ≠ 0 olan ikinci dereceden denklemleri çözmek için kullanılır. Bu formül aracılığıyla toplam (S) ve çarpım () için bir ifade çıkarabiliriz. 2. derece denklemin köklerinin P ).
Bhaskara formülü nedir?
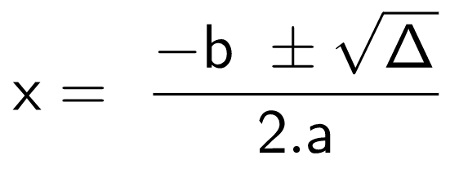
Bu Bhaskara formülü, 2. derece denklemlerin genel formülünden kaynaklanmıştır.
ax2 + bx + c = 0
sıfır olmayanlarla;
Öncelikle hesaplamanın tüm üyelerini 4a ile çarpıyoruz:
4a2x2 + 4abx + 4ac = 0;
Daha sonra aşağıdaki örnekte olduğu gibi her ikisine de b2'yi ekliyoruz.
4a2x2 + 4abx + 4ac + b2 = b2;
Bundan sonra yeniden gruplanırız:
4a2x2 + 4abx + b2 = b2 – 4ac
Dikkat ederseniz ilk üye tam kare bir üç terimlidir:
(2ax + b)² = b² – 4ac
Her iki tarafın karekökünü alıyoruz ve negatif ve pozitif kök olasılığını ortaya koyuyoruz. Sonra bilinmeyen x'i yalnız bırakırız, hepsi bu.
