ANNONCES
Bhaskara, formule Bhaskara
Nous connaissons tous Bhaskara comme la formule mathématique, mais savez-vous qui est le créateur de cette formule qui porte le nom de ce grand mathématicien ? Savez-vous également comment calculer la formule Bhaskara ?
Si vous ne connaissez pas très bien aucune des deux choses et que vous souhaitez en savoir plus sur Bhaskara, vous êtes au bon endroit, restez avec nous dans cet article et approfondissez vos connaissances sur les mathématiques et l'histoire de cette formule. .
ANNONCES
Qui était Bhaskara ?
Bhaskara était un mathématicien, astrologue, astronome et enseignant indien. Il est devenu connu pour avoir créé la formule mathématique appliquée à l'équation du 2e degré, bien qu'il existe une controverse à ce sujet.
Bhaskara est né dans la ville de Vijayapura, en Inde, un lieu avec une excellente tradition de mathématiciens. Son père était astronome et lui enseigna les principes des mathématiques et de l'astronomie.
Il dirigeait l'observatoire astronomique d'Ujjain, une école de mathématiques réputée. Bhaskara était un spécialiste des études algébriques, ce qui l'a amené à approfondir ses recherches sur les équations et les systèmes numériques.
ANNONCES
Bhaskara a travaillé sur la question de la racine carrée dans les équations, sachant qu'il y avait deux racines dans la résolution de l'équation quadratique, mais il n'existe aucune preuve solide que la formule bien connue de Bhaskara était en réalité la sienne. En effet, jusqu'au XVIe siècle, les équations comportaient des lettres, qui ont été utilisées après ce siècle par le mathématicien français François Viète.
La formule de Bhaskara et son histoire
Le nom Bhaskara's Formula a été créé pour rendre hommage au mathématicien Bhaskara Akaria. C'était un mathématicien, professeur, astrologue et astronome indien, considéré comme le mathématicien le plus important du XIIe siècle et le dernier mathématicien médiéval important en Inde.
La formule de Bhaskara permet de résoudre des équations quadratiques de formule générale ax² + bx + c = 0, à coefficients réels, avec a ≠ 0. C'est grâce à cette formule que l'on peut déduire une expression pour la somme (S) et le produit ( P ) des racines de l’équation du 2ème degré.
Quelle est la formule Bhaskara ?
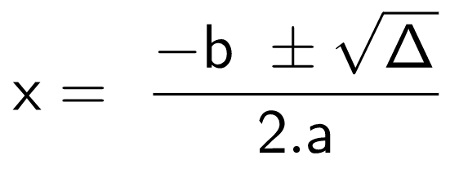
Cette formule de Bhaskara est issue de la formule générale des équations du 2e degré.
ax2 + bx + c = 0
avec non nul ;
Tout d'abord, nous multiplions tous les membres du calcul par 4a :
4a2x2 + 4abx + 4ac = 0 ;
Ensuite, nous ajoutons b2 aux deux, comme dans l’exemple ci-dessous.
4a2x2 + 4abx + 4ac + b2 = b2 ;
Après cela, nous regroupons :
4a2x2 + 4abx + b2 = b2 – 4ac
Si vous remarquez, le premier membre est un trinôme carré parfait :
(2ax + b)² = b² – 4ac
Nous prenons la racine carrée des deux côtés et introduisons la possibilité d’une racine négative et positive. Ensuite on isole l'inconnu x et c'est tout.
