ADVERTENTIES
Bhaskara, Bhaskara-formule
We kennen Bhaskara allemaal als de wiskundige formule, maar weet jij wie de maker was van deze formule die de naam draagt van deze grote wiskundige? Weet jij ook hoe je de Bhaskara-formule berekent?
Als je een van de twee dingen niet zo goed kent en dit en nog veel meer over Bhaskara wilt leren, ben je hier aan het juiste adres, blijf bij ons in dit artikel en vergroot je kennis over wiskunde en de geschiedenis rond deze formule .
ADVERTENTIES
Wie was Bhaskara?
Bhaskara was een Indiase wiskundige, astroloog, astronoom en leraar. Hij werd bekend door het creëren van de wiskundige formule die werd toegepast in de tweedegraadsvergelijking, hoewel er controverse bestaat over dit feit.
Bhaskara werd geboren in de stad Vijayapura, India, een plaats met een uitstekende traditie van wiskundigen. Zijn vader was astronoom en leerde hem de principes van wiskunde en astronomie.
Hij was hoofd van het astronomisch observatorium in Ujjain, een bekende wiskundeschool. Bhaskara was een specialist in algebrastudies, wat hem ertoe bracht zijn onderzoek naar vergelijkingen en numerieke systemen te verdiepen.
ADVERTENTIES
Bhaskara werkte aan de kwestie van de vierkantswortel in vergelijkingen, wetende dat er twee wortels waren bij het oplossen van de kwadratische vergelijking, maar er zijn geen harde bewijzen dat Bhaskara's bekende formule daadwerkelijk de zijne was. Dit komt omdat vergelijkingen tot de 16e eeuw letters hadden, die na die eeuw werden gebruikt door de Franse wiskundige François Viète.
Bhaskara's formule en zijn geschiedenis
De naam Bhaskara's Formula is gemaakt om hulde te brengen aan de wiskundige Bhaskara Akaria. Hij was een Indiase wiskundige, leraar, astroloog en astronoom, beschouwd als de belangrijkste wiskundige van de 12e eeuw en de laatste belangrijke middeleeuwse wiskundige in India.
De formule van Bhaskara wordt gebruikt om kwadratische vergelijkingen op te lossen met de algemene formule ax² + bx + c = 0, met reële coëfficiënten, met a ≠ 0. Via deze formule kunnen we een uitdrukking afleiden voor de som (S) en het product ( P ) van de wortels van de tweedegraadsvergelijking.
Wat is de Bhaskara-formule?
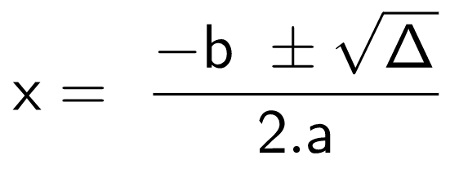
Deze Bhaskara-formule is ontstaan uit de algemene formule van tweedegraadsvergelijkingen.
ax2 + bx + c = 0
met niet-nul;
Eerst vermenigvuldigen we alle leden van de berekening met 4a:
4a2x2 + 4abx + 4ac = 0;
Vervolgens voegen we b2 aan beide toe, zoals in het onderstaande voorbeeld.
4a2x2 + 4abx + 4ac + b2 = b2;
Daarna hergroeperen we:
4a2x2 + 4abx + b2 = b2 – 4ac
Als je het opmerkt, is het eerste lid een perfecte vierkante trinominaal:
(2ax + b)² = b² – 4ac
We nemen de wortel van beide kanten en introduceren de mogelijkheid van een negatieve en een positieve wortel. Dan isoleren we de onbekende x en dat is alles.
