REKLAMA
Bhaskara, formuła Bhaskary
Wszyscy znamy Bhaskarę jako wzór matematyczny, ale czy wiecie, kto był twórcą tego wzoru, który nosi imię tego wielkiego matematyka? Czy wiesz także jak obliczyć wzór Bhaskary?
Jeśli nie znasz zbyt dobrze żadnej z tych dwóch rzeczy, a chcesz dowiedzieć się tego i wiele więcej o Bhaskarze, jesteś we właściwym miejscu, zostań z nami w tym artykule i poszerz swoją wiedzę na temat matematyki i historii otaczającej tę formułę .
REKLAMA
Kim był Bhaskara?
Bhaskara był indyjskim matematykiem, astrologiem, astronomem i nauczycielem. Zasłynął dzięki stworzeniu wzoru matematycznego stosowanego w równaniu II stopnia, choć fakt ten budzi kontrowersje.
Bhaskara urodził się w mieście Vijayapura w Indiach, miejscu o doskonałej tradycji matematyków. Jego ojciec był astronomem i nauczył go zasad matematyki i astronomii.
Był kierownikiem obserwatorium astronomicznego w Ujjain, znanej szkoły matematycznej. Bhaskara był specjalistą w dziedzinie algebry, co skłoniło go do pogłębienia badań nad równaniami i systemami numerycznymi.
REKLAMA
Bhaskara pracował nad pierwiastkiem kwadratowym w równaniach, wiedząc, że w rozwiązaniu równania kwadratowego występują dwa pierwiastki, ale nie ma solidnych dowodów na to, że dobrze znany wzór Bhaskary był w rzeczywistości jego autorstwa. Dzieje się tak dlatego, że równania aż do XVI wieku miały litery, których po tym stuleciu używał francuski matematyk François Viète.
Formuła Bhaskary i jej historia
Nazwa Formuła Bhaskary powstała na cześć matematyka Bhaskary Akarii. Był indyjskim matematykiem, nauczycielem, astrologiem i astronomem, uważanym za najważniejszego matematyka XII wieku i ostatniego ważnego średniowiecznego matematyka w Indiach.
Wzór Bhaskary służy do rozwiązywania równań kwadratowych za pomocą ogólnego wzoru ax² + bx + c = 0, ze współczynnikami rzeczywistymi, z a ≠ 0. Z tego wzoru możemy wydedukować wyrażenie na sumę (S) i iloczyn ( P ) pierwiastków równania II stopnia.
Jaka jest formuła Bhaskary?
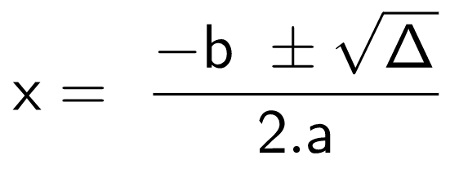
Ta formuła Bhaskary wywodzi się z ogólnego wzoru równań drugiego stopnia.
ax2 + bx + c = 0
z niezerowym;
Najpierw mnożymy wszystkie elementy obliczenia przez 4a:
4a2x2 + 4abx + 4ac = 0;
Następnie do obu dodajemy b2, jak w przykładzie poniżej.
4a2x2 + 4abx + 4ac + b2 = b2;
Następnie ponownie grupujemy:
4a2x2 + 4abx + b2 = b2 – 4ac
Jeśli zauważysz, pierwszy człon jest doskonałym trójmianem kwadratowym:
(2ax + b)² = b² – 4ac
Bierzemy pierwiastek kwadratowy z obu stron i wprowadzamy możliwość pierwiastka ujemnego i dodatniego. Następnie wyodrębniamy nieznane x i to wszystko.
