ANNONCER
Bhaskara, Bhaskara Formel
Vi kender alle Bhaskara som den matematiske formel, men ved du, hvem der var skaberen af denne formel, der bærer navnet på denne store matematiker? Ved du også, hvordan man beregner Bhaskara-formlen?
Hvis du ikke ved nogen af de to ting særlig godt og ønsker at lære dette og meget mere om Bhaskara, er du på det rigtige sted, bliv hos os i denne artikel og øg din viden om matematik og historien omkring denne formel .
ANNONCER
Hvem var Bhaskara?
Bhaskara var en indisk matematiker, astrolog, astronom og lærer. Han blev kendt for at skabe den matematiske formel anvendt i 2. grads ligning, selvom der er kontroverser om dette faktum.
Bhaskara blev født i byen Vijayapura, Indien, et sted med en fremragende tradition for matematikere. Hans far var astronom og lærte ham principperne for matematik og astronomi.
Han var leder af det astronomiske observatorium i Ujjain, en velkendt matematikskole. Bhaskara var specialist i algebrastudier, hvilket fik ham til at uddybe sin forskning i ligninger og numeriske systemer.
ANNONCER
Bhaskara arbejdede med spørgsmålet om kvadratroden i ligninger, velvidende at der var to rødder i løsningen af andengradsligningen, men der er ingen solide optegnelser om, at Bhaskaras velkendte formel faktisk var hans. Det skyldes, at ligninger indtil det 16. århundrede havde bogstaver, som blev brugt efter det århundrede af den franske matematiker François Viète.
Bhaskaras formel og dens historie
Navnet Bhaskara's Formula blev skabt for at hylde matematikeren Bhaskara Akaria. Han var en indisk matematiker, lærer, astrolog og astronom, betragtet som den vigtigste matematiker i det 12. århundrede og den sidste vigtige middelaldermatematiker i Indien.
Bhaskaras formel bruges til at løse andengradsligninger med den generelle formel ax² + bx + c = 0, med reelle koefficienter, med a ≠ 0. Det er gennem denne formel, vi kan udlede et udtryk for summen (S) og produktet ( P ) af 2. grads ligningens rødder.
Hvad er Bhaskara-formlen?
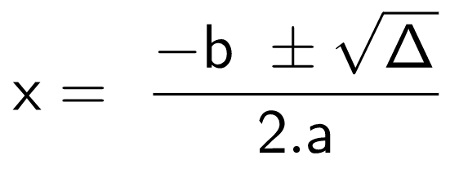
Denne Bhaskara-formel stammer fra den generelle formel for 2. grads ligninger.
ax2 + bx + c = 0
med ikke-nul;
Først gange vi alle medlemmer af beregningen med 4a:
4a2x2 + 4abx + 4ac = 0;
Så tilføjer vi b2 til begge, som i eksemplet nedenfor.
4a2x2 + 4abx + 4ac + b2 = b2;
Derefter omgrupperer vi:
4a2x2 + 4abx + b2 = b2 – 4ac
Hvis du bemærker, er det første medlem et perfekt kvadratisk trinomium:
(2ax + b)² = b² – 4ac
Vi tager kvadratroden af begge sider og introducerer muligheden for en negativ og en positiv rod. Så isolerer vi det ukendte x og det er det.
